纠结星人的胜利。
平凡栈实现
一谈起中缀表达式转前后缀表达式,网上的解决办法中,有一大半是用栈实现,我称之为平凡实现。因为这种方法总让我感觉是在头痛医头、脚痛医脚,拓展性不大。下面来看看。
中缀表达式转后缀表达式
原理
请原谅我很难把道理讲透,只能说说做法。大体上来看就是让操作符入栈,通过比较读取到的操作符和栈顶操作符优先级,进行入栈和出栈。
- 遇到操作数直接输出
- 遇到左括号,左括号入栈
- 遇到右括号,将pop到左括号为止
- 遇到操作符,把小于等于它优先级的操作符都出栈,直到左括号或者栈空,最后让它入栈
- 读取完表达式,将栈全部pop
示例
|
|
主要代码
数据结构:
实现代码:
中缀表达式转前缀表达式
原理
和转后缀很接近,但是稍麻烦些,需要从后往前读取,最后再翻转过来。而且优先级的比较和转后缀也有所不同,转后缀是小于等于,这里是小于。
- 从后向前读取表达式
- 遇到操作数直接输出
- 遇到右括号,右括号入栈
- 遇到左括号,将pop到右括号为止
- 遇到操作符,把小于它优先级的操作符都出栈,直到右括号或者栈空,最后让它入栈
- 读取完表达式,将栈全部pop
- 逆序输出
主要代码
|
|
结果

平凡二叉树实现
如果构造一棵语法树,那就想输出什么缀就输出什么缀,无非就是前序遍历和后序遍历。
像这样:
终端输出:
甚至可以画一棵二叉树:
终端输出:
原理
为什么又叫作平凡实现呢,因为这种实现在构造二叉树的时候,本质上和栈实现没太大差别,还是根据优先级进行入栈出栈。
主要代码
数据结构:
实现代码:
优雅实现之语法分析器
我实在是不满足平凡实现,觉得它太实在了,老老实实总会遭人欺负的。于是我对着这四则运算表达式圈圈画画,没想到还真看出来了端倪。然后赶紧上搜索引擎看看有没同道中人已经实现过这种思路,果然……轮子哥在八年前,也就是在我还是小学生的时候,就已经实现过了……好吧,下面一起来看看。
单位化
Exp
一个表达式,可以看成是若干个单位通过'+', '-'连接起来,比如:
我们把这种单位抽象出来,取个名字:Factor。
因此,表达式可以这样来表示: Exp = Factor (( '+' | '-' ) Factor)*,十分的简洁明了。
Factor
接下来Factor也不难表示,可以看成是若干个单位通过'*', '/'连接起来,比如:
我们把这种单位抽象出来,取个名字:Term。
因此,Factor可以这样来表示:Factor = Term (( '*' | '/' ) Term)*
Term
最后就是最基本的单位Term,通过观察可知Term要么是数字,要么是括号括起来的一个表达式:
因此Term可以这样来表示:Term = <数字> | '(' Exp ')'
我们可以通过上面的关系来构造语法树,可以想象,生成过程真的很像一棵树的生长。
没错!我就是想要这种非常函数式的实现,这种抽象美得让人陶醉。鲁迅先生好像说过:
Any problem in computer science can be solved with another level of indirection.
计算机科学里面,没有什么问题是多加一层抽象不可以解决的。
语法树特点
|
|
借用上边画出来的语法树,来观察语法树的结构:
- 一个数字表达式的节点一定是一个叶子节点,没有左右孩子节点。
- 一个二元运算表达式一定有两个孩子节点,因为二元运算符号左右两边必然都要有表达式。这两个叶子节点的类型,是抽象的表达式,既可以是二元运算表达式,也可以是数字表达式。
由此可以定义Expression作为基类,派生出NumberExpression类和BinaryExpression类,来表示数字表达式和二元运算表达式。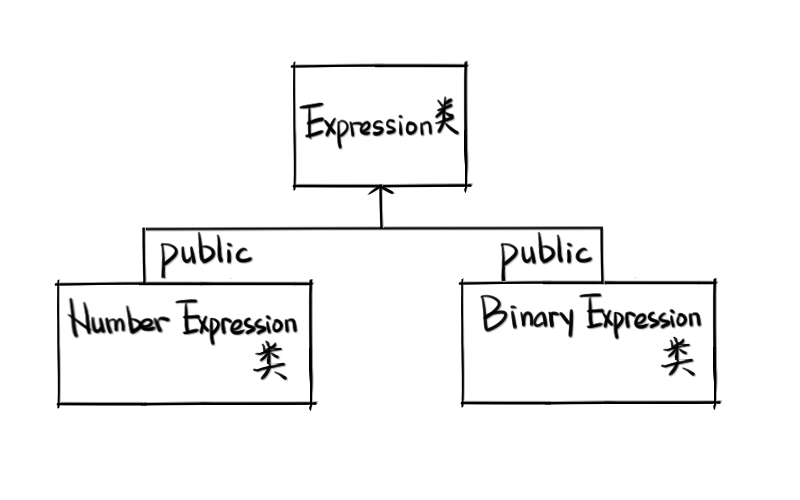
注:下面都是用现代C++来实现,区别于轮子哥八年前写的古老C++版。
|
|
BinaryOperator枚举类型也要现代一点:
构造语法树
辅助函数
Is
|
|
用于判断Stream是不是由Text开头,如果是就将Stream偏移strlen(Text)个字符。
GetNumber
|
|
这个函数的作用是,按照数字的方式,对Stream进行解析,如果解析成功,就将Stream指针的位置移动到解析完成的最后位置(代码中的Read),然后调用make_shared,构造一个shared_ptr并返回;而如果失败(即一个数字都没找到),则抛出一个异常。跟Is一样,这个函数会过滤掉开头的空格。
辅助异常类
|
|
核心代码
|
|
三个解析函数,完成语法树的构造。
GetExp
|
|
完成:Exp = Factor (( '+' | '-' ) Factor)*
构造出来的形状是这样的: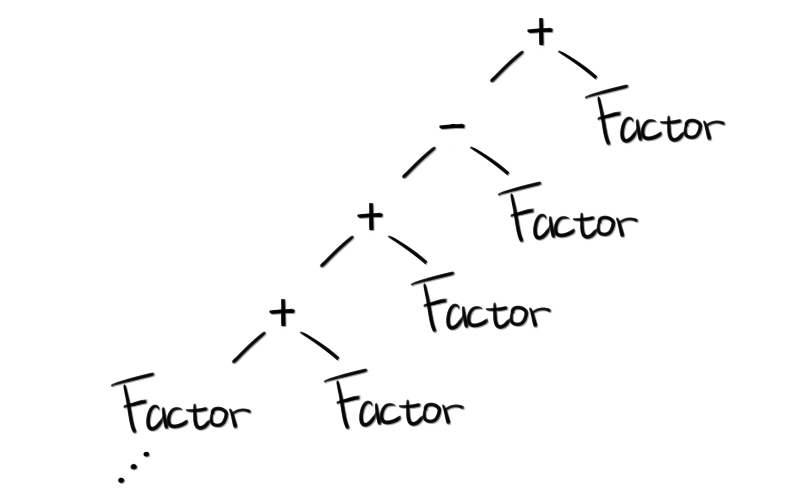
GetFactor
|
|
完成:Factor = Term (( '*' | '/' ) Term)*
GetTerm
|
|
完成:Term = <数字> | '(' Exp ')'
好了,这样就搞定啦!虽然代码看起来有点点长,可是思路是十分清晰自然的。我相信用函数式语言来写会短几十倍的,用C++写只是为了照顾大部分人。最后奉上测试代码。
测试代码
|
|
完整代码:https://gist.github.com/zhongzc/3f9cc3024684ab5b0b70729a348c5f6a