用C++写出伪LISP代码（二）

既已有基础材料，撸起袖子做作业。

---

什么都别说，先把用C++写出伪LISP代码（一）写的代码include进来：

#include "mylist.h"

---

作业要求

问题描述：
设计一个程序实现两个任意长的正数（包括正数和负数）、任意精度实数的算术运算；
提示：
（1）用动态链表存储数据，每节点含一个整型变量，表示若干位数；
（2）整数输入和输出按中国对于长整数的习惯表示，每3位1组，组间用逗号隔开；
（3）实现长整数的加、减运算；
（4）程序运行界面清晰实用；
选做：
（1）求两长整数之商、积
（2）高精度实数算术运算

---

最终成果

---

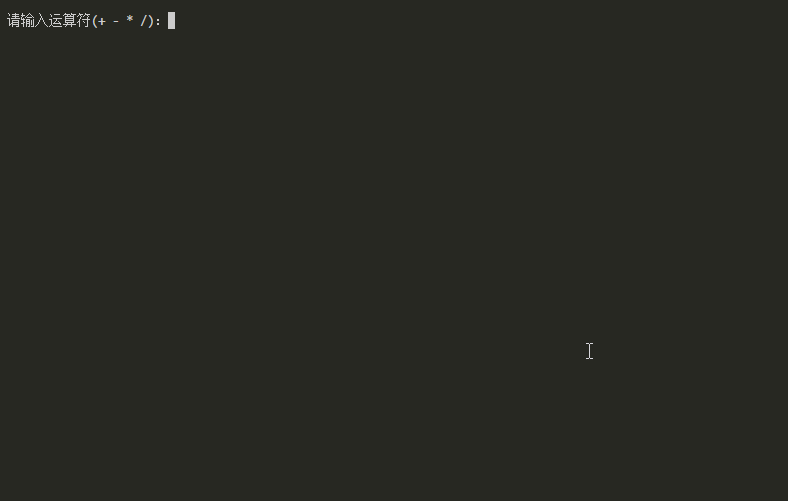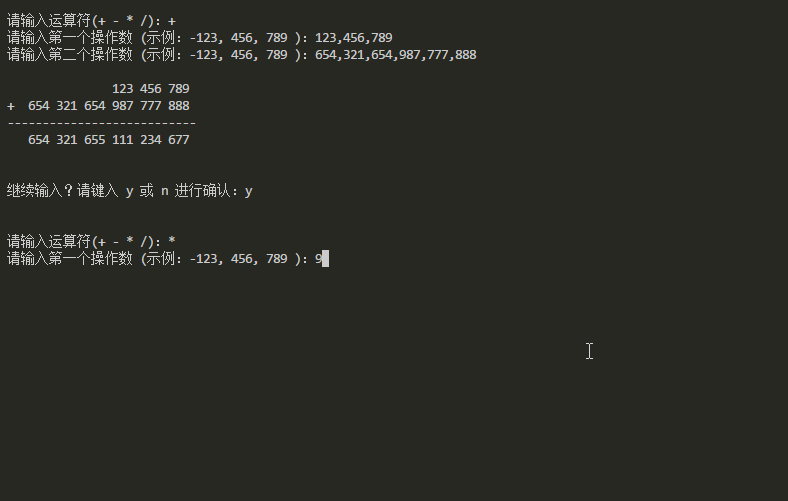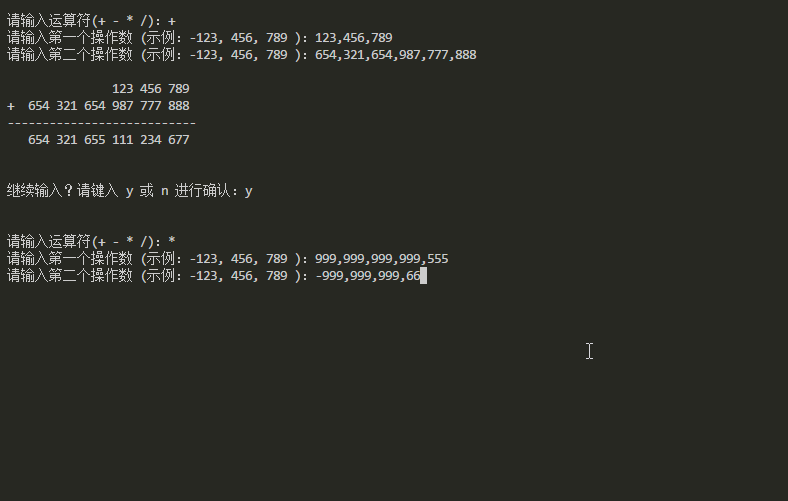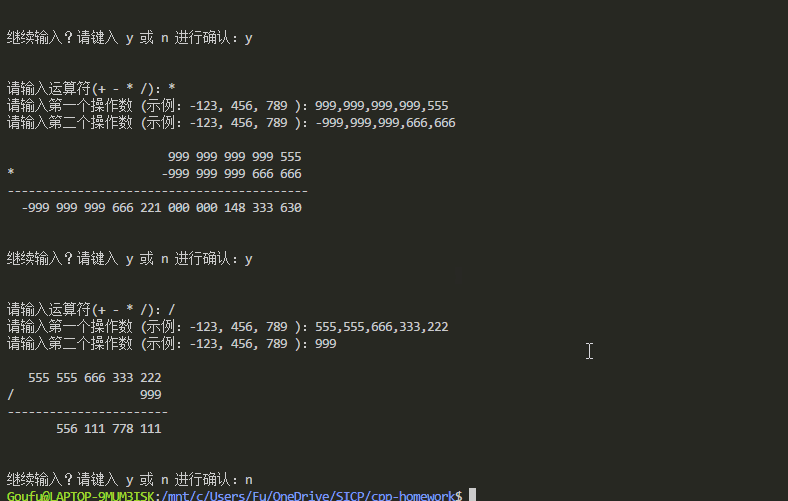
实现基础

要求3位3位地分割大数，对于我来说，很容易想到这是1000进制的加减乘除问题。因此问题转换成：如何实现任意进制的加减乘除。问题变得更通用，解决起来更有趣味和意义。

---

数据结构

既然是用伪LISP代码来完成，首先明确结构就应该是list，用每个盒子的head来存储该每3位数。定义如下：
(*注：以下所有C++代码均采用C++14标准)

using IntList = MyList<int>;
auto EmptyIntList = EmptyList<int>;

int base = 1000;
// 可以改成任意进制数，这里是1000进制
int highest_unit = base - 1;
// 每种进制的位最大表示数，如1000进制即999，10进制即为9，2进制即为1。

---

补码

接触过计算机组成原理的读者都知道，计算机内部采用二进制补码形式表示数字。用补码来表示数字，可以有效简化一些运算。
遗憾的是，用补码并不能解决溢出问题，两个很大的正数相加，有可能会造成溢出，导致数位的循环，得到负数的结果。造成这样的结果原因是每个数字都只由有限的数位表示，一旦某些运算企图逾越这些数位的限制，便要承担运算错误的风险。
我决定也采用补码来进行进制运算，来获得运算的简化。但尽管我是在模拟进制运算，也采用补码，却由于可以动态申请内存，因此消除了溢出的风险，从而实现长整数运算。

至于什么是补码？简单地说：

• 正数采用原有表示，但最高位添加符号位，为0。
• 0用0表示。
• 负数无视符号位，将所有位取反，再加1，最后最高位添加符号位，为进制最大表示数。

想更为深入地了解何谓补码、为何用补码运算能简化计算，推荐阅读《编码》。

在这里，用一个list来存储一个补码表示的数字，最前面为最低位，list最深处则为最高位。

因此直接通过最高位来判断补码的正负性：

bool is_negative(IntList n)
{
  int sign_digit = Reverse(n)->head();
  return sign_digit >= (base / 2);
}
// 这里放宽了条件，理论上最高位应该只可能是0或者进制最大表示数

---

位操作

补充与抛弃

IntList fill_low_digit(IntList, int, size_t);
IntList fill_high_digit(IntList, int, size_t);
IntList clip_high_digit(IntList, size_t);
IntList clip_low_digit(IntList, size_t);

补充

补充低位操作，这个较简单，直接往最前面填需要填充的数字即可：

// n: 补码  filler: 填充的数字  count: 填充位数
IntList fill_low_digit(IntList n, int filler, size_t count)
{
  return (count == 0) ? n : Cons(filler, fill_low_digit(n, filler, count - 1));
}

补充高位操作，则需要翻转一下list，然后利用上面刚实现的函数：

// n: 补码  filler: 填充的数字  count: 填充位数
IntList fill_high_digit(IntList n, int filler, size_t count)
{
  return Reverse(fill_low_digit(Reverse(n), filler, count));
}

抛弃

抛弃高位，由于有自带的ListHead函数，可以直接调用：

// n: 补码  count: 抛弃位数
IntList clip_high_digit(IntList n, size_t count)
{
  return ListHead(n, Length(n) - count);
}

抛弃低位，同理：

// n: 补码  count: 抛弃位数
IntList clip_low_digit(IntList n, size_t count)
{
  return ListTail(n, count);
}

算术左移与右移

IntList shift_left(IntList, size_t);
IntList shift_right(IntList, size_t);

算术左移

可以直接抛弃高位，低位补0：

// n: 补码  count: 左移位数
IntList shift_left(IntList n, size_t count)
{
  return fill_low_digit(clip_high_digit(n, count), 0, count);
}

算术右移

抛弃低位，高位补充符号位：

// n: 补码  count: 右移位数
IntList shift_right(IntList n, size_t count)
{
  return raise_digits(clip_low_digit(n, count), Length(n));
}

raise_digits是用于提升位数的，这里只是借用。提升位数本质上是补充符号位的操作，补充符号位并不影响数值表示大小，下面来实现：

位数提升

// n: 补码  target_digits_length: 目标位数长度
IntList raise_digits(IntList n, size_t target_digits_length)
{
  auto pre_len{Length(n)};
  if (pre_len > target_digits_length) {
    return n;
  }
  else {
    auto count{target_digits_length - pre_len};
    return is_negative(n) ?
      fill_high_digit(n, highest_unit, count) :
      fill_high_digit(n, 0, count);
  }
}

注意，如果目标位数长度大于原位数长度，则不进行提升，直接返回原数。

取反

取反的意思是将每一位都取成进制最大表示数与其之差。取反需要遍历，遍历需要fold：

IntList invert(IntList n)
{
  return FoldRight([](int x, IntList xs) { return Cons(highest_unit - x, xs); }, 
                       EmptyIntList, n);
}

进位

进位的重要性不言而喻，要保证进位后每一个位都不能超过进制最大表示数：

int calc_carry(int n) { return n / base; }
// 用于计算某个位需要往高位进几
int calc_remain(int n) { return n % base; }
// 用于计算某个位实际应当存放的数
IntList carry(IntList n, int x)
{
  if (x == 0) {
    return n;
  }
  else if (n == EmptyIntList) {
    return EmptyIntList;
  }
  else {
    auto neW{n->head() + x};
    auto new_last_digit{calc_remain(neW)};
    auto new_carry{calc_carry(neW)};
    return Cons(new_last_digit, carry(n->tail(), new_carry));
  }
}

取负

这个大家都应该很熟悉了，取负的操作 —— 取反加一！

IntList negate(IntList n)
{
  return carry(invert(n), 1);
}

---

补码构造

实现了各种位操作，终于可以用来构造补码了。
用户输入的正数形式为123, 456, 789，存储成list即为(123, 456, 789)，正好与补码形式相反，因此只需补充符号位，再翻转list即可。
负数形式为-123, 456, 789，存储成list即为(-123, 456, 789)，这里将第一位变成正数，借用构造正数的过程，最后再取负。
实现如下：

IntList make_number(IntList lst)
{
  if (Any([](int x) -> bool { return x < 0; }, lst->tail())) {
    throw std::runtime_error("###### 操作数输入错误：符号错误。");
  }
  else if (Any([=](int x) -> bool { return abs(x) >= base; }, lst)) {
    throw std::runtime_error("###### 操作数输入错误：每单元最多包含3位数。");
  }
  else {
    return (lst->head() >= 0) ?
      Reverse(Cons(0, lst)) :
      negate(make_number(Cons(- lst->head(), lst->tail())));
  }
}

---

加减乘除

IntList add(IntList, IntList);
IntList sub(IntList, IntList);
IntList mul(IntList, IntList);
IntList div(IntList, IntList);

该来的还是来了。

加法

补码加法就是可以为所欲为，只需要位数相同，无视正负数直接加。当位数不同时，提升位数后再加。学过全加器的读者应该能看出add(carry(x->tail(), new_carry)是多么亲切。

IntList add(IntList x, IntList y)
{
  auto x_len{Length(x)};
  auto y_len{Length(y)};
  if (x_len != y_len) {
    auto higher_digits_length = x_len > y_len ? x_len : y_len;
    return add(raise_digits(x, higher_digits_length),
               raise_digits(y, higher_digits_length));
  }
  else if (x == EmptyIntList && y == EmptyIntList) {
    return EmptyIntList;
  }
  else {
    auto neW{x->head() + y->head()};
    auto new_last_digit{calc_remain(neW)};
    auto new_carry{calc_carry(neW)};
    return Cons(new_last_digit, add(carry(x->tail(), new_carry), y->tail()));
  }
}

---

减法

传说中的开挂来了，不多说。

IntList sub(IntList x, IntList y)
{
  return add(x, negate(y));
}

---

乘法

先实现一位乘以多位，接着实现多位乘以多位。计算过程和手动乘法差不多，注意到一位乘以多位可以直接用Map，多位乘以多位用到了Fold配合左移。
有读者可能会问，这不是补码吗，为什么这里感觉像是直接原码乘。是的，这里实际上采用的是补码一位乘的校正法，是我从华工编写的《计算机组成原理与汇编语言》里面找来的。最后还需要看情况补上一个余项。至于这个余项怎么算出来，读者可以自己翻书（笔者数学不好实在是搞不懂）。

IntList mul(IntList x, IntList y)
{  
  auto mul_digit_by_all_digits = [](int x, IntList xs) {
      return PoorMap([=](int y) { return y * x; }, xs);
    };

  auto mul_digits_by_all_digits = [&mul_digit_by_all_digits](IntList y, IntList x) {
      return FoldRight([=, &mul_digit_by_all_digits](int term, IntList xs) {
          return add(mul_digit_by_all_digits(term, y),
                     shift_left(xs, 1));
      }, make_number(toList({0})), x);
    };
  
  auto new_digits_length{Length(x) + Length(y) - 1};
  auto pre_mul = [=](IntList x, IntList y) { 
      return mul_digits_by_all_digits( raise_digits(x, new_digits_length), y);
    };

  auto remain_term = [=](IntList t1, IntList t2) {
      return !(is_negative(t2)) ?
        make_number(toList({0})) :
        negate( shift_left( raise_digits(t1, new_digits_length),
                            Length(t2)));
    };
  // 传说中神奇的余项

  return add(pre_mul(x, y), remain_term(x, y));
}

---

除法

到了除法，我已经越来越懒于找更精妙的算法了。全部转成正数，直接仿照人工手动除法，最后再调整符号。
quo_prime和rem_prime两个函数用于最初级的除法形式：被除数减除数，重复减直至负数，减的次数即为商。
当然不可能真的这样来计算商，我们可以先通过calc_digits计算商的位数，然后模仿人工除法，把除数左移，然后再利用quo_prime和rem_prime一位一位算。

IntList div(IntList x, IntList y)
{
  if (Length(Filter([](int x) { return x != 0; }, y)) == 0) {
    throw std::runtime_error("###### 除零错误。");
  }

  std::function<int(IntList, IntList)> quo_prime = 
  [&quo_prime](IntList t1, IntList t2) {
    auto remain{sub(t1, t2)};
    return is_negative(remain) ? 
      0 : (1 + quo_prime(remain, t2));
  };
  std::function<IntList(IntList, IntList)> rem_prime = 
  [&rem_prime](IntList t1, IntList t2) {
    auto remain{sub(t1, t2)};
    return is_negative(remain) ?
      add(remain, t2) : rem_prime(remain, t2);
  };


  std::function<int(IntList, IntList)> calc_digits = 
  [&calc_digits](IntList t1, IntList t2) {
    return is_negative(sub(t1, t2))?
      0 : (1 + calc_digits(t1, shift_left(t2, 1)));
  };

  auto div_posi = [&calc_digits, &quo_prime, &rem_prime](IntList t1, IntList t2) {
    auto raised_t2 = raise_digits(t2, Length(t1));
    auto digits_length = calc_digits(t1, raised_t2);

    auto result = make_number(toList({0}));
    for ( auto dividend = t1
        , divisor = shift_left(raised_t2, digits_length - 1)
        ; digits_length != 0
        ; digits_length--)
        {
          result = Cons(quo_prime(dividend, divisor), result);
          dividend = rem_prime(dividend, divisor);
          divisor = shift_right(divisor, 1);
        }
    return result;
  };


  if (is_negative(x) && is_negative(y)) {
    return div_posi(negate(x), negate(y));
  }
  else if (is_negative(x)) {
    return negate(div_posi(negate(x), y));
  }
  else if (is_negative(y)) {
    return negate(div_posi(x, negate(y)));
  }
  else {
    return div_posi(x, y);
  }
}

到这里，所有核心代码已经交代完毕，剩余的就是些交互代码了。交互代码可以放松对函数式的执着，毕竟全是在跟副作用打交道！

---

交互代码

最后再来实现一个REPL（Read–Eval–Print Loop）。

读取（Read）

IntList Parser(std::string s)
{
  std::string delimiter{","};

  IntList result{EmptyIntList};

  size_t pos{0};
  std::string token;
  while ((pos = s.find(delimiter)) != std::string::npos) {
      token = s.substr(0, pos);
      result = Cons(stoi(token), result);
      s.erase(0, pos + delimiter.length());
  }
  
  return Reverse(Cons(stoi(s), result));
}

求值（Eval）

IntList Eval(char op, IntList x, IntList y)
{
  switch (op) {
    case '+': return add(x, y); break;
    case '-': return sub(x, y); break;
    case '*': return mul(x, y); break;
    case '/': return div(x, y); break;
    default: return EmptyIntList; break;
  }
}

打印（Print）

打印函数是整个程序中第二长的函数，可见为了用户体验，程序员付出了多少汗水。

void PrettyPrint(char op, IntList left, IntList right, IntList result)
{
  auto format_num = [](IntList n) -> IntList {
    auto remove_zero = [](IntList n) -> IntList {
      auto a = n;
      for (
          ; (a->head() == 0) && (a->tail() != EmptyIntList)
          ; a = a->tail()
      ) {}
      return a;
    };
    if (is_negative(n)) {
      auto posi = remove_zero(Reverse(negate(n)));
      return Cons(- posi->head(), posi->tail());
    }
    else {
      return remove_zero(Reverse(n));
    }
  };
  auto l = format_num(left);
  auto r = format_num(right);
  auto res = format_num(result);
  auto len = std::max({Length(l), Length(r), Length(res)});

  auto print_num = [](IntList n, size_t len) -> void {
    auto print_digit = [](int n, size_t width) -> void {
      std::cout << std::setfill('0') << std::setw(width) << n;
    };

    std::cout << std::setfill(' ') << std::setw(4 * (len - Length(n)) + 1) << ' ';
    std::cout << std::setfill(' ') << std::setw(4) << n->head();
    while (n->tail() != EmptyIntList) {
      std::cout << " ";
      n = n->tail();
      print_digit(n->head(), 3);
    }
  };

  std::cout << std::endl << " ";  
  print_num(l, len);
  std::cout << std::endl << op;
  print_num(r, len);
  std::cout << std::endl << std::setfill('-') << std::setw(4 * (len + 1)) << ' ';
  std::cout << std::endl << " ";
  print_num(res, len);
  std::cout << std::endl;
}

ONE LOOP

void Engine()
{
  std::cout << "\n\n请输入运算符(+ - * /)：";
  char op;
  std::cin >> op;
  std::string junk;
  std::getline(std::cin, junk, '\n');
  if (op != '+' && op != '-' && op != '*' && op != '/' ) {
    throw std::runtime_error("###### 操作符解析错误：应为 + 或 - 或 * 或 /。");
  }

  std::cout << "请输入第一个操作数 (示例：-123, 456, 789 )：";
  std::string s1{""};
  std::getline(std::cin, s1, '\n');
  auto n1 = make_number(Parser(s1));

  std::cout << "请输入第二个操作数 (示例：-123, 456, 789 )：";
  std::string s2{""};
  std::getline(std::cin, s2, '\n');  
  auto n2 = make_number(Parser(s2));

  if (Length(n1) <= 0 || Length(n2) <= 0) {
    throw std::runtime_error("###### 操作数解析错误，格式应为：-123, 456, 789");
  }

  auto res = Eval(op, n1, n2);
  PrettyPrint(op, n1, n2, res);
}

REPL 以及错误处理

int main()
{
  while (1) {
    try {
      Engine();
    }
    catch (std::runtime_error err) {
      std::cerr << "\n" << err.what() << "\n";
    }
    std::cout << "\n\n继续输入？请键入 y 或 n 进行确认：";
    char c;
    if (!(std::cin >> c) || c == 'n') break;
  }
  return 0;
}

---

作业一到此为止，作业二更有意思，让我们拭目以待。
完整代码：https://github.com/zhongzc/C-/blob/master/longnum.cpp

---