编译原理学习笔记（一）

记录

---

文法的形式化定义

G = (V_T, V_N, P , S )

各成分含义

• V_T：终结符集合
  • 终结符（terminal symbol）是文法所定义的语言的基本符号，有时也称为token
  • 例：V_T = { apple, boy, eat, little }

• V_N：非终结符集合

  • 非终结符 ( nonterminal ) 是用来表示语法成分的符号，有时也称为“语法变量”

  • 例: V_N = { <句子>, <名词短语>, <动词短语>, <名词>, … }

    V_T ∩ V_N = Φ
    V_T ∪ V_N = 文法符号集

• P：产生式集合

  • 产生式 ( production ) 描述了将终结符和非终结符组合成串的方法
  • 产生式的一般形式： α→β ，读作：α定义为β
    • α∈(V_T ∪ V_N )⁺，且α中至少包含V_N中的一个元素：称为产生式的头 ( head ) 或左部 ( left side )
    • β∈(V_T ∪ V_N )^*：称为产生式的体(body)或右部(right side)
  • 例：{<句子>→<名词短语><动词短语>,<名词短语>→<形容词><名词短语>,……}
• S：开始符号
  • S∈V_N 。开始符号 ( start symbol ) 表示的是该文法中最大的语法成分
  • 例：S = <句子>

---

• 例子：

  G = ({id, +, *, (, )}, {E}, P, E)
  P = {	E → E + E,
  	E → E * E,
  	E → ( E ),
  	E → id}

  约定：不引起歧义的前提下，可以只写产生式

  G : 	E → E + E
  	E → E * E
  	E → ( E )
  	E → id

  简写：

  G : E → E + E | E * E | ( E ) | id

---

符号约定

• 终结符
  • 字母表中排在前面的小写字母，如 a、b、c
  • 运算符，如 +、*等
  • 标点符号，如括号、逗号等
  • 数字 0、1、… 、9
  • 粗体字符串，如id、if等
• 非终结符
  • 字母表中排在前面的大写字母，如A、B、C
  • 字母S。通常表示开始符号
  • 小写、斜体的名字，如 expr、stmt等
  • 代表程序构造的大写字母。如E(表达式)、T(项)和F(因子)
• 文法符号（即终结符或非终结符）
  • 字母表中排在后面的大写字母（如X、Y、Z）
• 终结符号串
  • 字母表中排在后面的小写字母（主要是u、v、… 、z）
• 文法符号串
  • 小写希腊字母，如α、β、γ
• 除非特别说明，第一个产生式的左部就是开始符号

---

语言的定义

推导和归约

用产生式的右部替换产生式的左部，称为推导 (Derivations)

如果α0=>α1，α1=>α2，α2=>α3，…，α n-1=>αn，则可以记作α0=>α1=>α2=>α3=> …=> α n-1=>αn，称符号串 α0经过n步推导出αn，可简记为α0=>ⁿαn

用产生式的左部替换产生式的右部，称为归约 (Reductions)
例：

<句子> => <名词短语><动词短语>
       => <形容词><名词短语><动词短语>
       => little <名词短语><动词短语>
       => little <名词><动词短语>
       => little boy <动词短语>
       => little boy <动词><名词短语>
       => little boy eats <名词短语>
       => little boy eats <名词>
       => little boy eats apple

由上往下是推导，由下往上是归约

---

句型和句子

• 如果 S=>*α, α∈(V_T∪V_N)*，则称α是G的一个句型(sentential form)
• 如果 S=>*w，w∈V_T*，则称w是G的一个句子(sentence)

句子是不包含非终结符的句型

• 由文法G的开始符号S推导出的所有句子构成的集合称为文法G生成的语言，记为L(G)。

---

Chomsky 文法分类体系

0型文法 (Type-0 Grammar)

• 无限制文法(Unrestricted Grammar) / 短语结构文法(Phrase Structure Grammar, PSG )
  • ∀α → β∈P， α中至少包含1个非终结符

PSG中可包含ε-产生式

---

1型文法 (Type-1 Grammar)

• 上下文有关文法(Context-Sensitive Grammar , CSG )
  • ∀α → β∈P，｜α｜≤｜β｜
  • 产生式的一般形式： α1Aα2 → α1βα2 ( β≠ε )

CSG中不包含ε-产生式

---

2型文法 (Type-2 Grammar)

• 上下文无关文法 (Context-Free Grammar, CFG )
  • ∀α → β∈P，α ∈ V_N
  • 产生式的一般形式：A→β

---

3型文法 (Type-3 Grammar)

• 正则文法 (Regular Grammar, RG )
  • 右线性(Right Linear)文法： A→wB 或 A→w
  • 左线性(Left Linear) 文法： A→Bw 或 A→w

---

四种文法之间的关系

逐级限制：

• 0型文法：α中至少包含1个非终结符
• 1型文法（CSG） ：｜α｜≤｜β｜
• 2型文法（CFG） ：α ∈ V_N
• 3型文法（RG）：A→wB 或 A→w (A→Bw 或A→w)

---

CFG的分析树

分析树举例

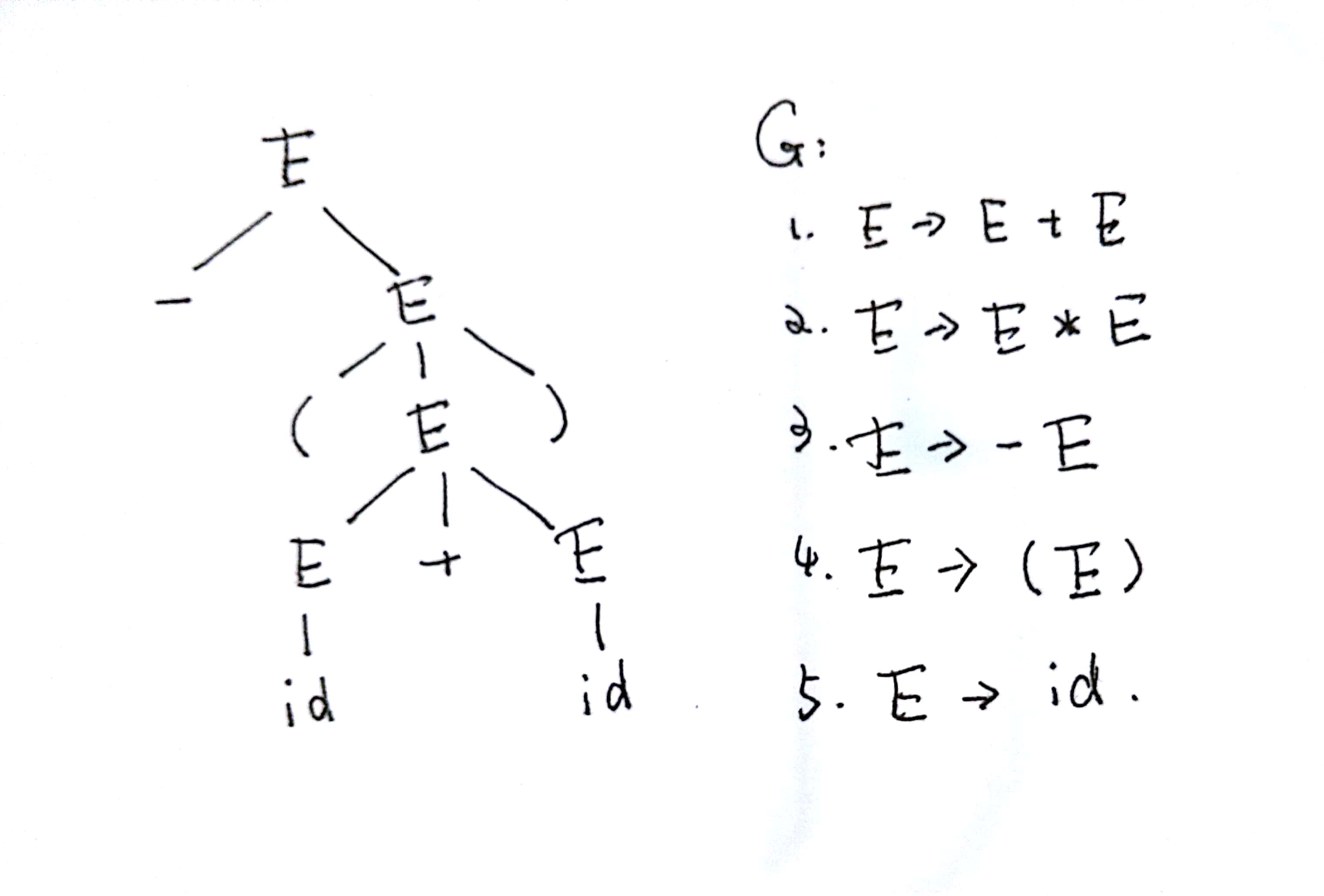
• 分析树是推导的图形化表示
  推导过程：E => -E => - ( E ) => - ( E+E ) => - ( id+E ) => - ( id+id )
• 结构
  • 根节点的标号为文法开始符号
  • 内部结点表示对一个产生式A→β的应用，该结点的标号是此产生式左部A。该结点的子结点的标号从左到右构成了产生式的右部β
  • 叶结点的标号既可以是非终结符，也可以是终结符。从左到右排列叶节点得到的符号串称为是这棵树的产出(yield)或边缘(frontier)

---

二义性文法

如果一个文法可以为某个句子生成多棵分析树，则称这个文法是二义性的

例：
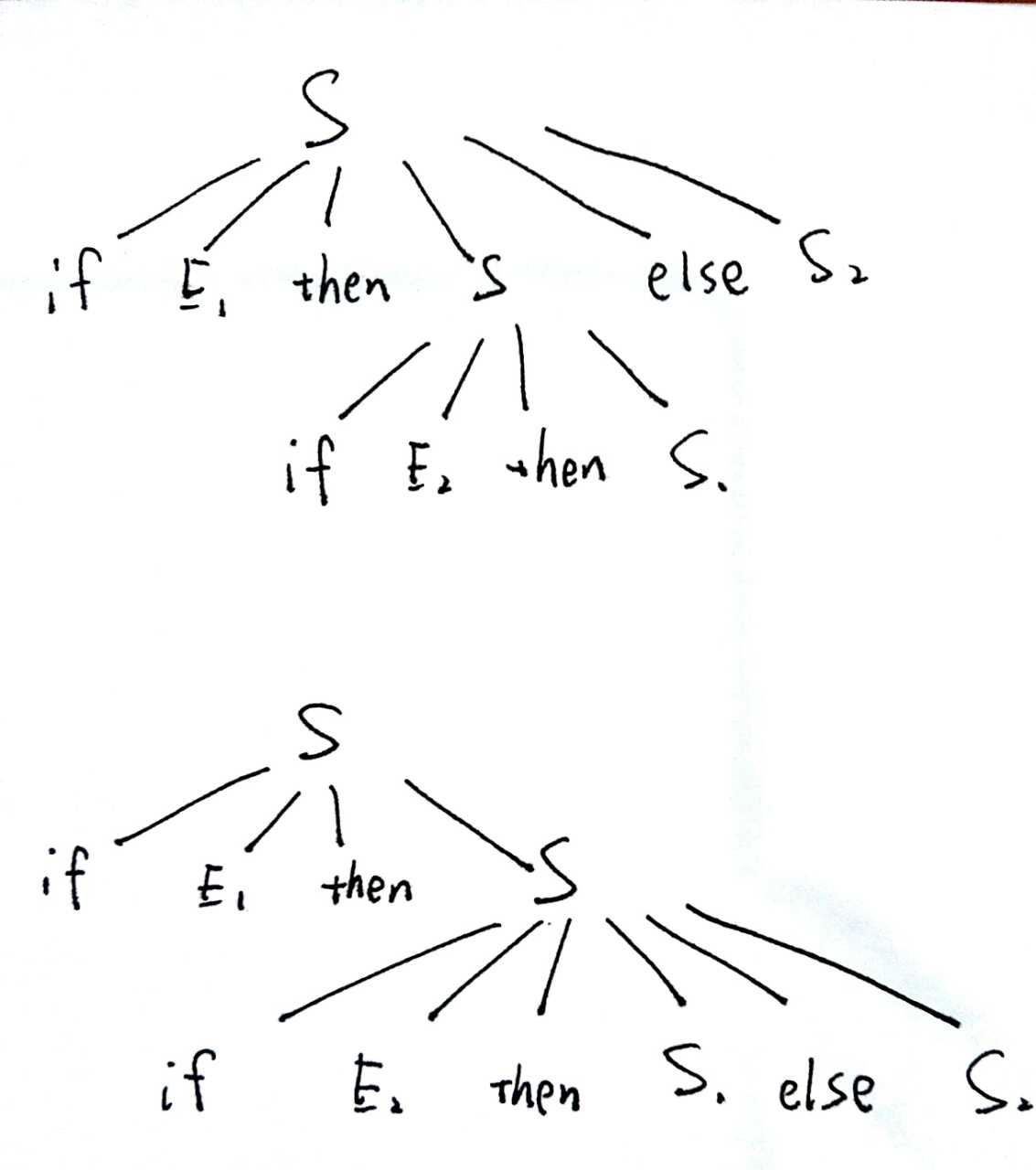
文法：S → if E then S | if E then S else S | other
句型：if E1 then if E2 then S1 else S2
可生成的分析树有：

---